The Pulfrich Effect: Text Explanation by Alfred Lit

Copyright (c) 1960, Alfred Lit. Permission of the author and the publisher is granted to make (download) a single copy of this explanation for personal, noncommercial use. All other rights are reserved.
Modification or redistribution of all or part of this work in any form is forbidden: Please contact the author for permission to post or copy this work for any purpose.

This explanation is adapted from Lit (1960) on target thickness. Please refer to that paper, posted elsewhere at this web site, for further information. Lit's (1949) classic, also posted at this web site, explains the geometry in full detail.

Alfred Lit (1960), paraphrased:

The stereoscopic effect with which the present experiment deals was first described and analyzed by Pulfrich in 1922. A target which is oscillating at eye level in a frontoparallel plane appears to rotate out of its plane of oscillation when a neutral or colored filter is placed in front of one of the observer's eyes.

The depth effect becomes noticeable at some threshold difference of binocular retinal illuminance and progressively increases as the difference of binocular retinal illuminance is increased.

Pulfrich (following a suggestion by Fertsch) accounted for these depth displacements in terms of a difference in the hypothesized visual latent periods of the two eyes. The visual latent period of each eye was assumed to be a reciprocal function of the prevailing level of retinal illuminance. Thus, the eye covered with the filter presumably "signals" a position of the oscillating target that lags behind the position signaled by the uncovered eye. Hence, at any given moment, synchronous binocular signals are provided by pairs of noncorresponding retinal points in the two eyes, and the magnitude of the stereoeffect theoretically depends on the amount of the retinal disparity produced as a consequence of the difference in the visual latent periods of the two eyes.

In Lit's work, the appearance of the targets to an observer, with the upper target in motion, would be as in this figure, or in this animation:

Consider the geometry, viewed from above, shown in in the next figure, of a target that is oscillating in a frontoparallel plane with constant linear velocity V for the central portion of its stroke.

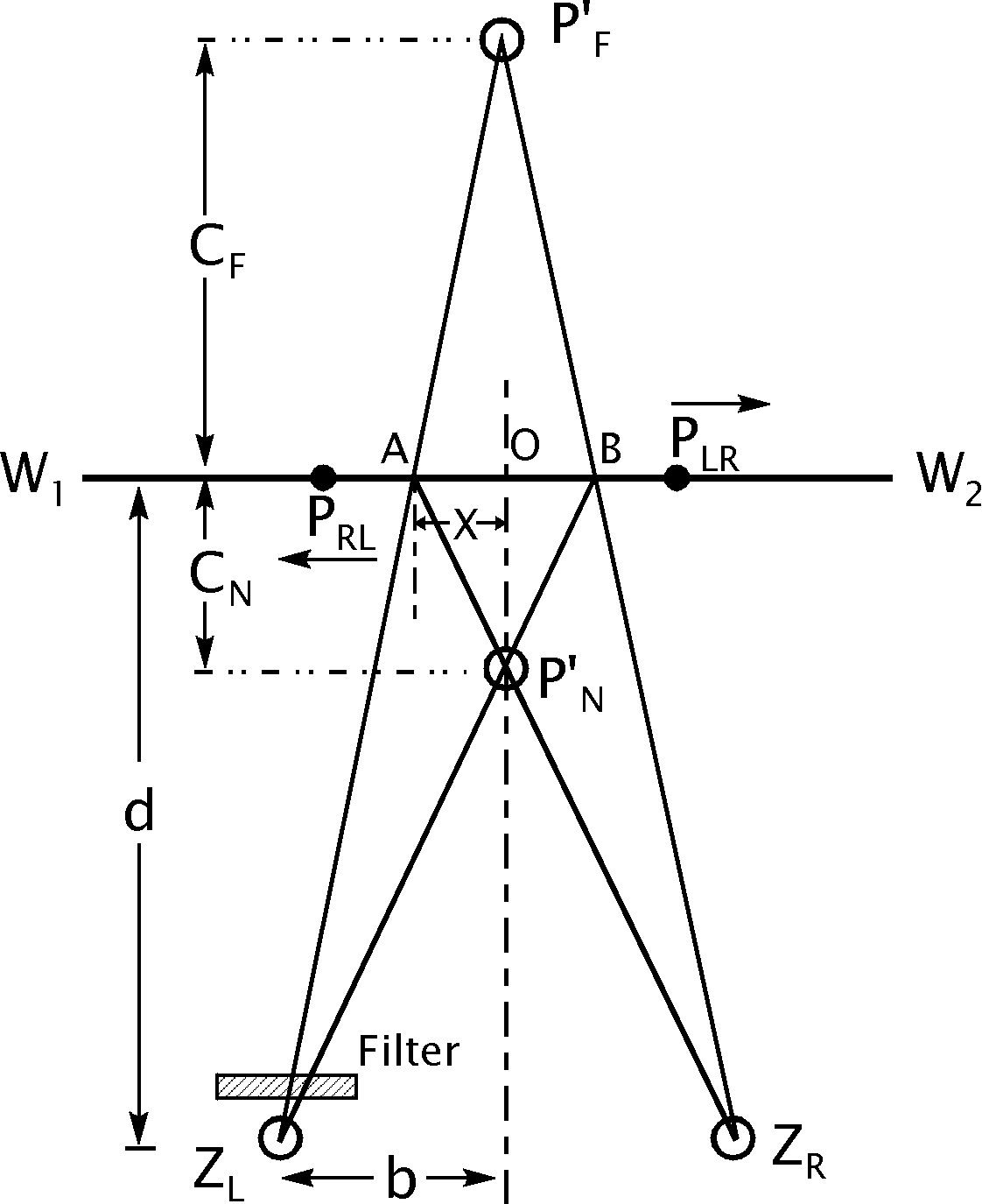
The linear path of the target in its plane of oscillation is denoted by W₁W₂. The distance d of the plane of oscillation is measured from the midpoint of the line Z_LZ_R which joins the centers of rotation of the two eyes.

As indicated, the filter is placed in front of the left eye. The point P_F' represents the far position in the vertical median plane at which the oscillating target, at point P_LR, is localized by the observer as the target moves from left to right. The point P_N' represents the near position of localization in the vertical median plane when the target, moving from right to left, has reached the point P_RL. The distance OP_F' designates the magnitude of the far displacement C_F. The distance OP_N' designates the magnitude of the near displacement C_N.

In accordance with the laws of binocular space discrimination, lines of sight from each eye are drawn through the two respective points of target localization, P_F' and P_N'. The intersection points of the lines of sight with the line W₁W₂ are designated by A and B, and these points theoretically mark the respective positions in the path of the oscillating target at which onset of stimulation occurred in each of the two eyes.

Thus, when the target is moving from left to right and appears to be located at the far position P_F' towards which the eyes are converged, the onset of stimulation for the right eye occurs when the target (at P_LR in the diagram) is located at point B, and the onset of stimulation for the left eye, covered by the filter, occurs when the target is located at point A, a bit farther behind in its path.

The time taken for the target to move from B to P_LR represents the magnitude of the visual latent period of the right eye, and the time taken for the target to move from A to P_LR represents the slightly longer visual latent period of the left eye.

Consequently, the time taken for the target to move from A to B represents the difference, , in the visual latent periods of the two eyes, based on the far position of target localization, P_F'. It follows by the same reasoning that when the target is moving from right to left and appears to be located at the near position, P_N', towards which the eyes are now converged, the time taken for the target to move from B to A represents the difference, , in the visual latent periods of the two eyes, based on the near position of target localization, P_N'. An animation may help visualization of these quantities.

It can be readily seen from similar triangles in the diagram above that for target localizations at P_N' and P_F', respectively:

where X=1/2 the distance from A to B, and b=1/2 the distance between the centers of rotation of the two eyes.

For an oscillating target moving with constant linear velocity V, the time taken for the target to pass through the distance X is given by the formula

The time taken for the target to move from A to B (or B to A) represents the difference, , in the visual latent periods of the two eyes. Since =2t, we obtain from Eq. (2)

By substituting for X the respective expressions given in Eq. (1), we finally obtain the following relationships between the experimentally determined near and far displacements (C_N and C_F) and the corresponding near and far latency differences ( and ):

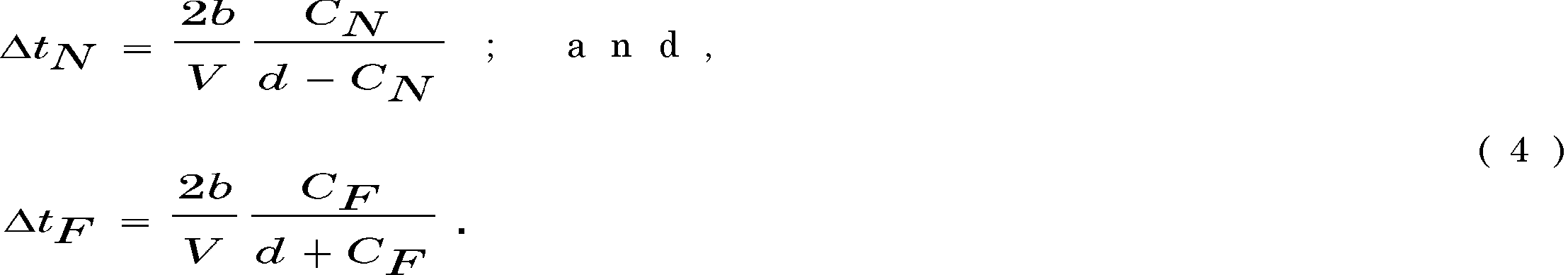
It should be noted from purely geometric considerations that, for any constant difference of binocular retinal illuminance, the magnitude of the stereoscopic effect as measured by C_N and C_F should progressively increase as the linear velocity of the oscillating target is increased, but the corresponding calculated values of and should remain constant for all target velocities used.

Email Comments.

Back to Pulfrich Effect Home. University Privacy Policy