Physics of c: Proof

Preliminary Assumptions

We shall begin by assuming all operations to occur in vacuum and far from any object capable of exerting a measurable gravitational force.

We shall use the word "object" to refer to an elementary particle or other thing which may be localized and which may be affected as a whole by some other object, the interaction occurring at an identifiable location but without regard for rotation or resolution of substructure of any object.

We allow for clocks to synchronize events, an event being the coincidental observation of one or more objects in the same place as the clock. We allow distance to be measured (by units of length) between events.

We assume no object can move at infinite speed, or causality (ordering of effects) would not be possible.

We shall allow any object either to be accelerable or inaccelerable but never both.

Definition of Accelerability

An accelerable object is any one which can be made to move at different velocities, depending on what is done to affect its motion.

Definition of an Inertial Frame

An inertial frame, or briefly, a frame, is a coordinate system attached to the motion of an accelerable object so that the object is at rest in that frame. Given such an inertial frame, then, if a force be exerted on the object, it will be accelerated so it is in motion in that frame; if no force be exerted, the object will remain at rest in that frame.

Definition of Inaccelerability

Objects that are inaccelerable always travel at a fixed speed, possibly zero, relative to every accelerable object, and at a fixed velocity relative to any given inertial frame.

Observation: Light is Inaccelerable

The experiment of Michelson and Morley, and the calculations of Maxwell, show that light (photons) is inaccelerable. We assume here, that when light is reflected or refracted, photons may be affected by the reflecting or refracting object so that they vanish and are replaced after some little time by others with the same speed but different velocity (direction).

An Inaccelerable Object Must Be Faster than any Accelerable One

Proof: Suppose an inaccelerable object I which travels at some speed v_I. Let I travel in some direction v, passing close to an accelerable object C located at x_i (i = initial). Let I continue and farther on pass equally close to a different accelerable object D located at x_f (f = final), both accelerable objects being at rest in the same frame but separated by a considerable distance in the direction v.

Now, let us repeat this observation but this time suppose that there might exist an accelerable object A allowing us exactly to copy the previous observation, with A substituted for I and travelling at speed v_A which is greater than, or equal to, v_I. If so, we could repeat yet a third time with both I and A starting at x_i together. But, I must travel at speed v_I in all inertial frames, including the rest frame of A, and so I must arrive at x_f before A. This contradicts the assumption that I travels at the same speed in all frames; therefore, no accelerable object can travel at a speed as great as that of an inaccelerable object.

The Speed of Every Inaccelerable Object is the Same

First, proof aside, if there were more than one speed for inaccelerable objects, they could change speed and therefore would not be inaccelerable. However, one might imagine that inaccelerable objects, like photons, never change between interactions and might then retain different speeds if created with different speeds. This very reasonable possibility is what requires the following:

Coarse Proof: Suppose two inaccelerable objects I and J could travel at different speeds v_I and v_J, with v_I greater than v_J. Start I, J, and an accelerable object A at the same time at x_i as above and in the direction v as above. Now, there is no reason why A could not be accelerated to a speed v_A just below that of I; therefore, a v_A could be reached such that v_I was greater than v_A and v_A was greater than v_J. But, this would be the same as allowing an accelerable object to move at a speed greater than that of the inaccelerable object J. Therefore, there can be no room between v_I and v_J for v_A, and both I and J must move at the same speed.

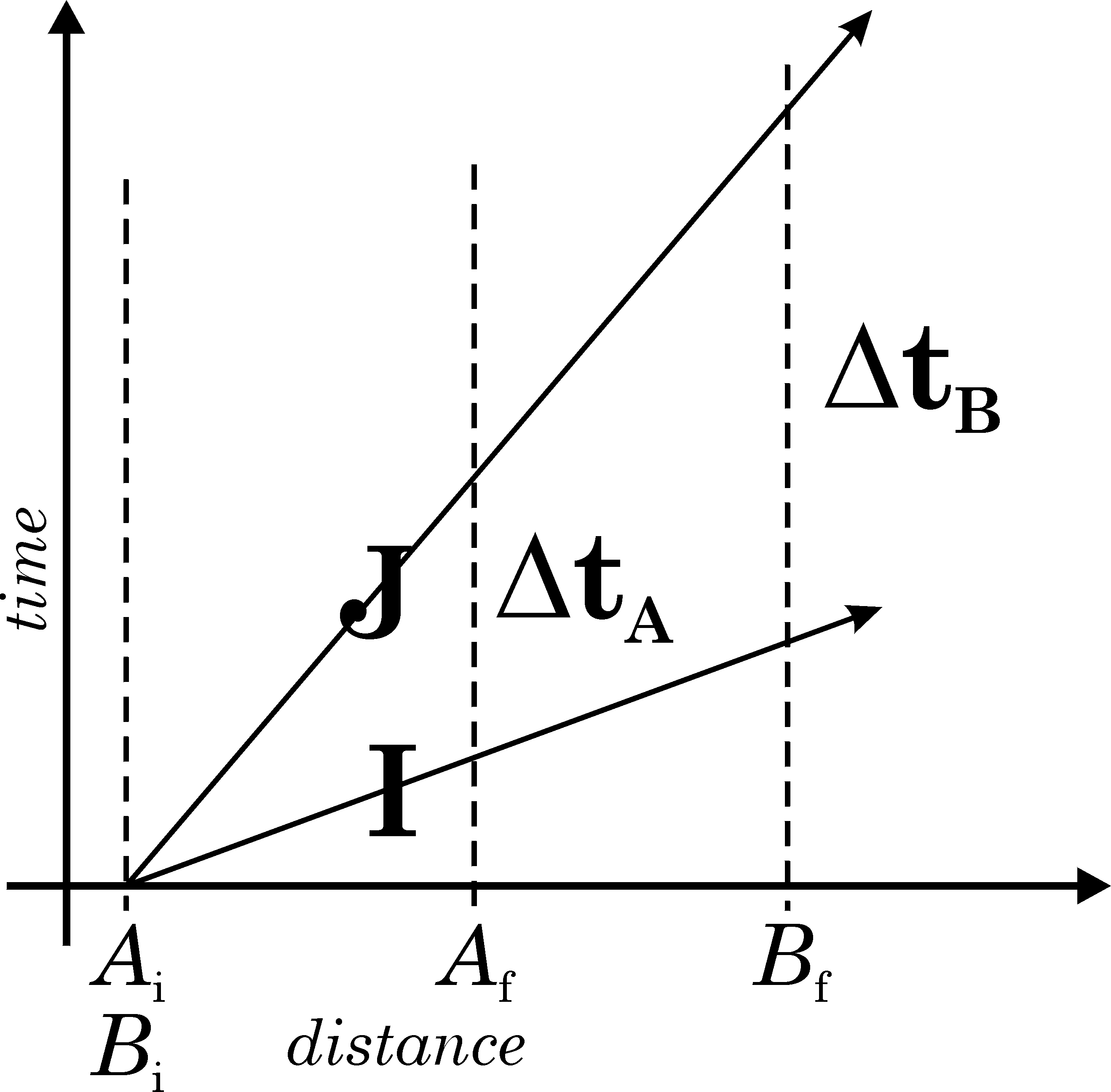
More Rigorous Proof: Let there exist two accelerable objects A_i and A_f initially at points x_i and x_f respectively in the same frame, such that the distance, L = x_f - x_i might be chosen to be large and well-defined in that frame. Let the direction of x_f - x_i be represented by the vector x.

Let there exist a different two accelerable objects B_i and B_f separated by the same distance L along the same distance vector but in a different frame which is in motion in the direction of x at some arbitrarily high speed relative to the frame of the A's.

Representing B_f as to the right of B_i, let B_f pass close to A_i and continue on, moving to the right. When B_i then passes close to A_i, let there be an emission event as follows:

At the same instant in both frames, A_i emits a pair of inaccelerable objects in the direction of A_f, and B_i emits an identical pair in the direction of B_f. Of course, the two direction vectors are the same. Let each pair of inaccelerable objects be called I and J, with, by hypothesis, the speed of I greater than that of J.

Now, because the distance between the A's is equal to that between the B's, and because inaccelerable objects travel at the same speeds in every inertial frame, both of A_f and B_f must receive a pair of I and J separated by the same time interval, delta-t, as measured in their respective frames.

Because by hypothesis the speed of an I is greater than that of a J, in both frames, the I's must arrive first. But, the frame of the B's is in motion relative to that of the A's, in the direction of the inaccelerable propagation, so the distance from A_i to B_f must increase (in both frames) while the inaccelerable objects are propagating. Therefore, the difference in arrival times between I and J at B_f must be greater than delta-t. See the figure.

The same quantity can not both be equal and not equal to delta-t, so the assumption implying delta-t must be invalid, and inaccelerable objects can not exist which travel at different speeds. All differences between such speeds must be identically 0. This makes delta-t equal to 0 regardless of relative motion of inertial frames, preventing the contradiction just derived.

We conclude that all inaccelerable objects move at the same speed c, in the frame of every accelerable object. And no object, accelerable or inaccelerable, can exceed the speed c in any frame.

The speed of light then equals this same c.

Email Comments.

Back to Pulfrich Effect Home. University Privacy Policy