The Pulfrich Effect: Animated Explanation

Copyright (c) 1998, Southern Illinois University. Permission is granted to make (download) a single copy of this page, and/or its animation, for personal, noncommercial use. All other rights are reserved.
Modification or redistribution of all or part of this work in any form is forbidden: Please contact the copyright owner for permission to post or copy this work for any purpose.

The animation on this page shows the geometry of the Pulfrich effect, as discussed by Alfred Lit on the text explanation pages elsewhere at this web site.

To see the animations, your browser must be capable of displaying 'GIF animations'. If you have Microsoft Explorer or Netscape Navigator version 2 or earlier, you may have to upgrade your browser.
GIF animation is built into the browser; but, be sure your browser is set up to "load images".

To make an animation repeat, use your browser's [reload] or [refresh] button. With some older browsers, the second animation (below) will repeat only by clicking on the link for the 'detailed' version, and then using [back] and [forward] buttons.
To stop an animation, use your browser's [stop] button.

In the first animation, the upper target is shown oscillating back and forth, just as an experimental observer would see it WITHOUT the Pulfrich filter in front of the left eye.

Note: These GIF animations depend on network and browser performance; they may not properly show that the target speed is constant and equal in either direction, left-to-right and right-to-left.

Because GIF animations are discrete frames and not physical motion, the Pulfrich effect can't be viewed on screen (above) as well as with a real moving target. However, an effect measuring apparently a couple of millimeters may be obtained using the animated target view above: View the animation above with the computer monitor at arm's length, with brightness turned down, and with a sunglass lens held before the left eye. It may take a few repeat cycles for the Pulfrich effect to become evident. Allowing the eyes to follow the (jerky) moving target may increase the magnitude of the illusion, although usually Lit's experiments have been done with the eyes fixated on the lower target.
To see the actual Pulfrich effect, suspend a small weight from a string, swing it in a pendulum arc, and hold one lens of a pair of sunglasses in front of the left eye. Of course, just putting on the sunglasses will affect vision about equally in both eyes, and no Pulfrich effect will be obtained.
Some of the Java-animated web sites listed in the external link pages may give smoother target motion in a web browser, but real moving targets always will be best.
Also, note that in the animation above, the left and right extreme ends of the Lit target traversal are concealed from the observer. Observers in Lit's experimental procedure have no difficulty making settings near the MIDDLE of the target visible traverse; in practice, the end points don't matter. However, these end points are simulated in the geometry animations at this web site, to emphasize the geometrical relations and the latencies involved.

In the second animation, the view is from above, as though looking down on the experiment from the ceiling.

There are two copies of this animation, a smoother, more detailed version which is almost 200K bytes, and the quicker version located here, immediately below:

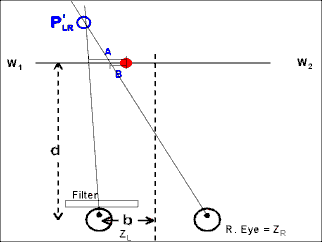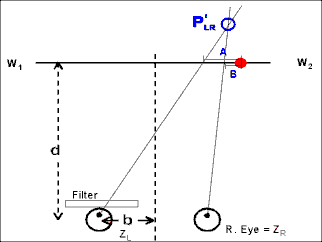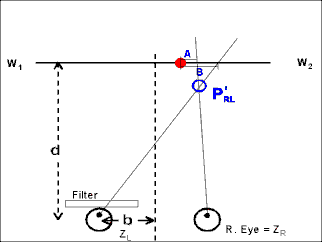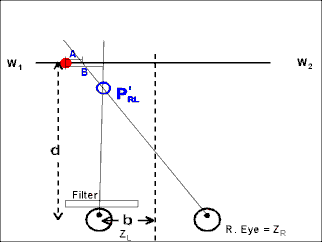
Again, the upper target is shown oscillating back and forth, as the filled circle. The lower target, which is set by the observer to P'_N or P'_F to match the apparent Pulfrich distance, is not shown.

The filled (red) circle shows where the observer would localize the target without any filter. The typical "personal equation" (localization error) is not shown.

The unfilled (blue) circle shows how the observer, with the Pulfrich filter in front of the left eye, would locate the target.

If the target motion were simple harmonic (sinusoidal), then the path would be an ellipse, as viewed from above, not the flattened curve shown in this animation.

Email Comments.

Back to Pulfrich Effect Home. University Privacy Policy